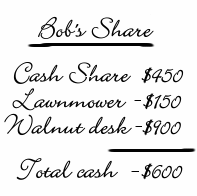|
First, create a cash account by adding together all of the amounts that the recipients must "pay" for the items they've won. Divide the total by the number of recipients.
Example: In the Snider family example, Bob won the lawn mower for $150 and the walnut desk for $900, while Mary won the ceramic horse for $300. Steve won nothing. Here's the cash account:
Now create "share accounts" for each of the recipients. At the top, put the recipient's share of the cash account. From that, subtract the second-highest bid prices of all of the items the recipient won. The net amount tells how much cash the recipients must give or receive in order to balance the shares.
Example:
|
|
|
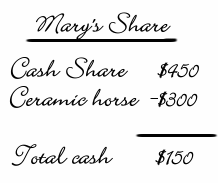 |
Steve ends up with $450 and no property. Bob gets the lawnmower and walnut desk, but he must pay $450 to Steve and $150 to Mary, for a total cash payout of $600. Mary gets the ceramic horse plus $150 cash.